Difference between revisions of "Hypothesis testing"
Ciskowski003 (talk | contribs) (→Hypothesis Testing) |
Ciskowskid (talk | contribs) (→Hypothesis Testing) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 8: | Line 8: | ||
*The claim about the population that we are trying to find evidence for is the '''alternative hypothesis''' (H<sub>a</sub>). | *The claim about the population that we are trying to find evidence for is the '''alternative hypothesis''' (H<sub>a</sub>). | ||
**A '''one-sided''' alternative hypothesis has the form H<sub>a</sub>: parameter < null value or H<sub>a</sub>: parameter > null value. | **A '''one-sided''' alternative hypothesis has the form H<sub>a</sub>: parameter < null value or H<sub>a</sub>: parameter > null value. | ||
| − | **A '''two-sided''' alternative hypothesis has the form H<sub>a</sub>: parameter | + | **A '''two-sided''' alternative hypothesis has the form H<sub>a</sub>: parameter ≠ null value. |
*Often, H<sub>0</sub> is a statement of no change or no difference. The alternative hypothesis states what we hope or suspect is true. | *Often, H<sub>0</sub> is a statement of no change or no difference. The alternative hypothesis states what we hope or suspect is true. | ||
*The '''P-value''' of a test is the probability of getting evidence for the alternative hypothesis H<sub>a</sub> that is as strong or stronger than the observed evidence when the null hypothesis H<sub>0</sub> is true. | *The '''P-value''' of a test is the probability of getting evidence for the alternative hypothesis H<sub>a</sub> that is as strong or stronger than the observed evidence when the null hypothesis H<sub>0</sub> is true. | ||
| Line 18: | Line 18: | ||
Reference: | Reference: | ||
| − | Daren, S. S., & Tabor, J. (2020). Updated version of the practice of Statistics (Teachers Edition) (Sixth Edition). W H FREEMAN & CO LTD. | + | Daren, S. S., & Tabor, J. (2020). ''Updated version of the practice of Statistics (Teachers Edition)'' (Sixth Edition). W H FREEMAN & CO LTD. |
''contributed by Katie Ciskowski'' | ''contributed by Katie Ciskowski'' | ||
| + | |||
| + | ==Test Statistic Formulas== | ||
| + | |||
| + | [[File:Test_Statistic_Formulas.PNG]] | ||
| + | |||
| + | ''contributed by David Ciskowski'' | ||
== == | == == | ||
Latest revision as of 10:34, 11 May 2022
Hypothesis Testing
A hypothesis test is a procedure for using observed data to decide between two competing claims, called hypotheses. The hypotheses are often statements about a parameter, like the population proportion p or the population mean μ. A hypothesis test is sometimes referred to as a significance test.
Hypothesis Testing: The Basics
- The claim that we weigh evidence against in a hypothesis test is called the null hypothesis (H0). The null hypothesis has the form H0: parameter = null value.
- The claim about the population that we are trying to find evidence for is the alternative hypothesis (Ha).
- A one-sided alternative hypothesis has the form Ha: parameter < null value or Ha: parameter > null value.
- A two-sided alternative hypothesis has the form Ha: parameter ≠ null value.
- Often, H0 is a statement of no change or no difference. The alternative hypothesis states what we hope or suspect is true.
- The P-value of a test is the probability of getting evidence for the alternative hypothesis Ha that is as strong or stronger than the observed evidence when the null hypothesis H0 is true.
- Small P-values are evidence against the null hypothesis and for the alternative hypothesis because they say that the observed result is unlikely to occur when H0 is true. To determine if a P-value should be considered small, we compare it to the significance level α.
- We make a conclusion in a hypothesis test based on the P-value.
- If P-value < α: Reject H0 and conclude there is convincing evidence for Ha (in context).
- If P-value > α: Fail to reject H0 and conclude there is no convincing evidence for Ha (in context).
Reference:
Daren, S. S., & Tabor, J. (2020). Updated version of the practice of Statistics (Teachers Edition) (Sixth Edition). W H FREEMAN & CO LTD.
contributed by Katie Ciskowski
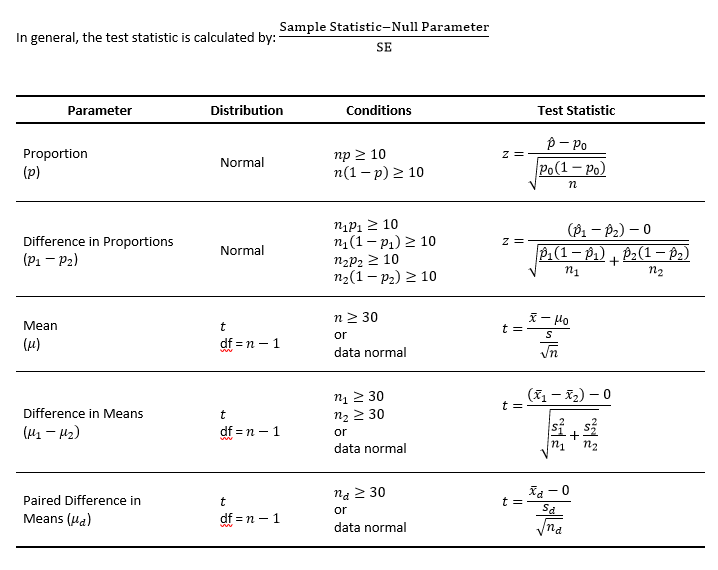
Test Statistic Formulas
contributed by David Ciskowski
The words probability and confidence seem to come up a lot. You should be getting the message that few things are definite in our discipline, or in any empirical science. Sometimes we get it wrong.
Type I Error
A level of significance of 5% is the rate you'll declare results to be significant when there are no relationships in the population. In other words, it's the rate of false alarms or false positives. Such things happen, because some samples show a relationship just by chance.
The only time you need to worry about setting the Type I error rate is when you look for a lot of effects in your data. The more effects you look for, the more likely it is that you will turn up an effect that seems bigger than it really is. This phenomenon is usually called the inflation of the overall Type I error rate, or the cumulative Type I error rate. So if you're going fishing for relationships amongst a lot of variables, and you want your readers to believe every "catch" (significant effect), you're supposed to reduce the Type I error rate by adjusting the p value downwards for declaring statistical significance.
The simplest adjustment is called the Bonferroni. For example, if you do three tests, you should reduce the p value to 0.05/3, or about 0.02. This adjustment follows quite simply from the meaning of probability, on the assumption that the three tests are independent. If the tests are not independent, the adjustment is too severe. For example, Bonferroni-adjusted 95% confidence intervals for three effects would each be 98% confidence.
Why not use a lower p value all the time, for example a p value of 0.01, to declare significance? Surely that way only one in every 100 effects you test for is likely to be bogus? Yes, but it is harder to get significant results, unless you use a bigger sample to narrow down that confidence interval. In any case, you are entitled to stay with a 5% level for one or two tests, if they are pre-planned--in other words, if you set up the whole study just to do these tests. It's only when you tack on a lot of other tests afterwards (so-called post-hoc tests) that you need to be wary of false alarms.
contributed by Karen Burke, EdD
Type II Error
The other sort of error is the chance you'll miss the effect (i.e. declare that there is no significant effect) when it really is there. In other words, it's the rate of failed alarms or false negatives. Once again, the alarm will fail sometimes purely by chance: the effect is present in the population, but the sample you drew doesn't show it.
The smaller the sample, the more likely you are to commit a Type II error, because the confidence interval is wider and more likely to overlap zero. The Type II error needs to be considered explicitly at the time you design your study. That's when you're supposed to work out the sample size needed to make sure your study has the power to detect anything useful. For this purpose, the usual Type II error rate is set to 20%, or 10% for really classy studies. The power of the study is sometimes referred to as 80% (or 90% for a Type II error rate of 10%). In other words, the study has enough power to detect the smallest worthwhile effects 80% (or 90%) of the time.
contributed by Karen Burke, EdD
Bias
People use the term bias to describe deviation from the truth. That's the way we use the term in statistics, too: we say that a statistic is biased if the average value of the statistic from many samples is different from the value in the population. To put it simply, the value from a sample tends to be wrong.
The easiest way to get bias is to use a sample that is in some way a non-random sample of the population: if the average subject in the sample tends to be different from the average person in the population, the effect you are looking at could well be different in the sample compared with the population.
Some statistics are biased, if we calculate them in the wrong way. Using n instead of n-1 to work out a standard deviation is a good example.
contributed by Karen Burke, EdD